All About Lines
Here you will be able to find basic, but detailed information on any topic related to lines
Parallel
Slope
Transversal
The Euclidean plane
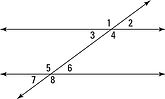
A transversal is a line that crosses over two other lines or more forming various different types of angles and angle pairs such as corresponding angles, vertical angles and alternate angles (click the tab all about angles to learn more about these specified)
These angles are formed when transversals are crossed over parallel lines, when a transversal is not crossed over parallel lines there are no specific properties to it.
The Euclidean plane is a two dimensional space of all real numbers and it is based on the principles of Euclidean Geometry such as the postulate that only one line can be drawn through a given point parallel through a given time.
Parallel lines theorem and
Perpendicular lines theorem.
Mid-point formula
Lines are parallel if and only if they never meet at any given point, and always stay the same distance away.
To prove lines are parallel we can use a transversal and see if any angles stated above in the description of transversals are formed (ie. supplementary angles)
If any of the following angles are formed when a transversal is used to cross over these two lines suspect of being parallel, we can affirm that they are in fact, parallel:
Corresponding angles
Alternate interior angles
Alternate exterior angles
Supplementary angles
All this can be solved as well in a two column proof, if you would like to sketch out any proof for that in order to achieve extra practice, please do so.
The slope is the measure of the steepness of a line which could also be called it's tilt. Slopes can be negative, positive or 0.
We determine slope by using the principle equation of rise/run where we basically put the change in y's over the change in x's and keep that as our slope.
the official formula for slope is
(y2 - y1) / (x2- x1)
A mid-point formula is used to find the exact middle point between two other points to find either the rest of a triangle, or a bisector.
The formula states that to find the mid-point you must find the average of both x and y coordinates. By this I mean find the average of the x-coordinates of both points of which you are trying to find the mid point, and that number would equal the x-coordinate of the new middle point. Repeat that with the y coordinate and thats how you find the mid point of the two points.
There are various theorems regarding both topics:
Parallel lines:
-
A common theorem states that parallel lines are cut by a transversal, the alternate interior angles are congruent and the same goes for exterior angles.
-
If two parallel lines are cut by a transversal, the corresponding respective angles are congruent to each other
-
If two parallel lines are cut by a transversal, then the two interior angles on the same side are supplementary
(all the above theorems can be flipped if beleived that it would be better adaped to the cause)
Perpendicular Lines:
-
In a plane, if a line is perpendicular to one of two parallel lines, then it is perpendicular to the other line as well.
-
