All About Polygons
What is a polygon?
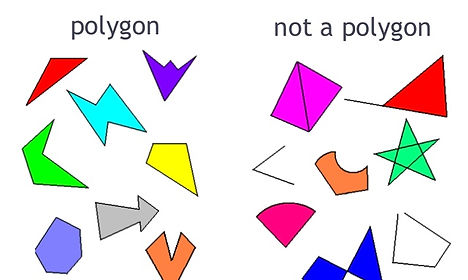
A polygon is a two dimensional shape with a specific checklist of characteristics:
-
Must be made of straight lines (no curves)
-
The shape must be closed.
-
At least 3 sides
-
Exactly two sides meet at every vertex
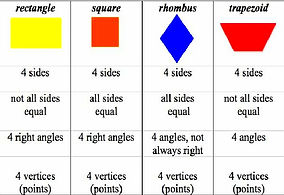
Quadrilateral
Sides of polygons and the relation to the degrees inside them
Grouping polygons/types
Vertices
-
Regular: is equiangular and equilateral.
-
Irregular: not equiangular nor equilateral
-
Concave: at least one of its internal angles is greater than 180 degrees
-
Convex: no internal angles are greater then 180 degrees
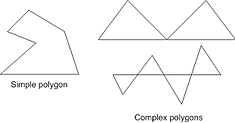
Simple and Complex polygons will be explained by the following picture:
A vertex is where every two lines meet on a polygon. (also where the angles form)
The vertices of a polygon are convex if all interior angles are less than 180. If there is even just one angle that is greater then 180, the vertices would be concaved.
There are ways to group types of polygons according to their vertices, as stated to the left
A quadrilateral is any polygon with 4 sides and therefore 4 angles and 4 vertices.
Examples could include a square, rectangles and parallelograms.
The basic principal is that the interior angles in certain type of regular polygon are always the same.
This could relate to the central angle theorem, where we divide 360 by the number of sides in a regular polygon to find out the central angle of a shape.
Ex. A square has 4 sides so we would divide 360 by 4 to get 90, which would be the measure of the central angle.
But there arealso ways to find out the entire shapes interior angles using the basic knowledge of triangles, because angles in a triangle always add up to 180, as you probably know.
So, starting from triangle, everytime a side is added on, you add 180 to the degrees of all angles of the shape added up.
So if there are 5 sides in a shape, it would be 180 (3 sides) + 2 more 180’s.
Which would equal 540 degrees
Another way to think of it is n (number of sides) minus 2, times 180.
(n-2)180
To find the measure of each separate angle we can use the same equation but divide the whole thing by the number of sides.
(N-2)180/n
You might be thinking, why do we subtract 2 from the number of sides?
Well its because we don’t start counting from a 1 sided polygon, because that doesn’t exist. We start counting 180 from a 3-sided polygon, a triangle, as we consider that the first step. So when we subtract 2 in the equation we are taking in consideration and counting the amount of sides starting from a triangle, as if a triangle was 1.