All about Triangles
Types of traingles and Sum theorum
Mid-point segment of a triangle (and trapazoid)
Triangles can be classifies into three groups according to their sides:
-
Equilateral: When all three sides are congruent
-
Isosceles: whet at least 2 sides are congruent
-
Scalene: when no sides are congruent
The triangle sum theorem states that the sum of the interior angles of a triangle will always add up to 180 regardless of the type of triangles and their classification; no exceptions.
This is a great example of how to prove this theorem, taken from this website below
http://www.ck12.org/geometry/Triangle-Sum-Theorem/lesson/Triangle-Sum-Theorem-Intermediate/
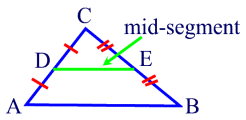
The mid-point segment of a triangle, also called a midline, is a segment joining the midpoints of two sides of a triangle so that it is parallel to the 3rd side and half the length of this same third side.
It is important to note that a triangle has 3 different possible midlines depending on what two sides of a triangle are joined. The line can be used as a reference to find other measurements
not given.
The midline of a trapazoid although has the same concept of joining two sides together, has different specifications. The mid-point segment of a trapazoid is the average of both bases in a trapazoid and because of this can be used to calculate area.